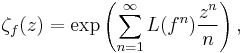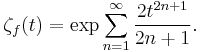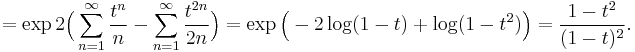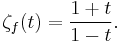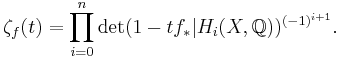Lefschetz zeta function

In mathematics, the Lefschetz zeta-function is a tool used in topological periodic and fixed point theory, and dynamical systems. Given a mapping ƒ, the zeta-function is defined as the formal series

\zeta_f(z) = \exp \left( \sum_{n=1}^\infty L(f^n) \frac{z^n}{n} \right),

where L(ƒ n) is the Lefschetz number of the nth iterate of ƒ. This zeta-function is of note in topological periodic point theory because it is a single invariant containing information about all iterates of ƒ.

Contents

Examples

The identity map on X has Lefschetz zeta function

1/(1 − t)χ(X),

where χ(X) is the Euler characteristic of X, i.e., the Lefschetz number of the identity map.

For a less trivial example, consider as space the unit circle, and let ƒ be its reflection in the x-axis, or in other words θ → −θ. Then ƒ has Lefschetz number 2, and ƒ2 is the identity map, which has Lefschetz number 0. All odd iterates have Lefschetz number 2, all even iterates have Lefschetz number 0. Therefore the zeta function of ƒ is

\zeta_f(t)=\exp \sum_{n=1}^\infty \frac{2t^{2n%2B1}}{2n%2B1}.

Via intermediate expressions

=\exp 2\Big(\sum_{n=1}^\infty \frac{t^n}{n}-\sum_{n=1}^\infty\frac{t^{2n}}{2n}\Big)=\exp \Big( -2\log(1-t)%2B\log(1-t^2)\Big)=\frac{1-t^2}{(1-t)^2}.

This is seen to be equal to

\zeta_f(t)=\frac{1%2Bt}{1-t}.

Formula

If f is a continuous map on a compact manifold X of dimension n (or more generally any compact polyhedron), the zeta function is given by the formula

\zeta_f(t)=\prod_{i=0}^{n}\det(1-t f_\ast|H_i(X,{\Bbb Q}))^{(-1)^{i%2B1}}.

Thus it is a rational function. The polynomials occurring in the numerator and denominator are essentially the characteristic polynomials of the map induced by f on the various homology spaces.

Connections

This generating function is essentially an algebraic form of the Artin–Mazur zeta-function, which gives geometric information about the fixed and periodic points of ƒ.

See also

References